Fat Man | guerre-mondiale

Fat Man quant à lui utilise une technique d’assemblage dite d’implosion. Cela consiste à placer un hémisphère sphérique de matière fissible de Plutonium 239 en bleu clair sur le schéma (avec un initiateur à neutron pour provoquer les réactions en chaîne) qui est entouré d’un autre hémisphère d’assemblage également sphérique de charges explosives classiques en jaune (toujours sur le schéma) qui sont reliées au détonateur à pression d’air (non représenté).

La bombe contient des lentilles explosives (qui se trouvent à l'extérieur de la "bande" d'explosifs classiques qu'on peut voir sur l'animation) et qui à pour but de modifier les ondes de détonation divergente en onde convergente vers l’intérieur de la bombe. C’est pourquoi une fois l’explosion des charges explosives grâce au détonateur à pression d’air, les lentilles explosives provoque la compression des explosifs puis du Plutonium 239 qui étaient jusque là en masse sub-critique et passeront en masses critique afin de commencer les réaction en chaine de Plutonium 239.

La détonation eut lieu à 550 mètres d'altitude, tuant plus de 70 000 civils.

Schéma de l'assemblage de la bombe Fat Man

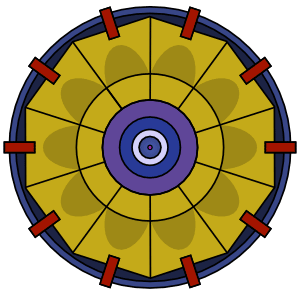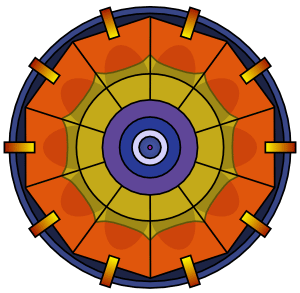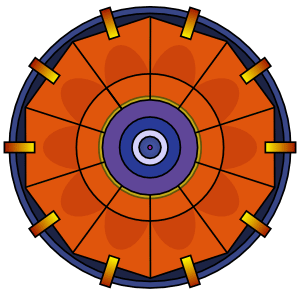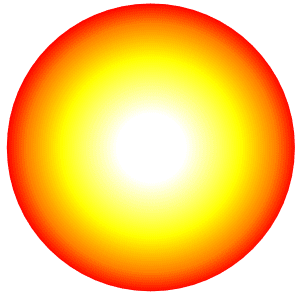
Animation montrant les lentilles explosives compressant les explosifs classique en jaune puis progressant jusqu'au coeur du Plutonium 239

Comme pour Little Boy, on fera en sorte que toutes les fissions donnaient cette même équation :

1

0

5

D'abord, calculons l'énergie libérée de cette réaction de fission nucléaire.

Soit m(Pu) = 239,052163u ; m(Mo) = 99,907477u ; m(Te) = 133,911369u ; m(n) = 1,0087u ; c = 3,0*10^8 m/s

D'où DE = /DM/*c² = [m(Mo)+m(Te)+5*m(n)-m(Pu)-m(n)]*c² = 1,198*1,66*10^-27*c² = 1,7906*10^-10 J

Calculons ensuite la masse d'un noyau de Plutonium 239. Il faut tout d'abord trouver la masse du noyau sachant que, pour le noyau de Plutonium 239, Z= 94 et A =239 d'où A-Z = 145. Masse d'un neutron : m(n)= 1,0087u Masse d'un proton : m(p)= 1,0073u D'où m(noyau) = Z*m(proton) + A-Z*m(neutron) D'où m(noyau Plutonium 239) = (94*1,0073+145*1,0087)*1,66*10^-27 = 3, 9998*10^-25 kg

Puis, il faut calculer le nombre de noyaux dans un gramme de Plutonium 239 (voir résonnement dans la rubrique Little Boy partie "L'énergie qu'elle libère"). D'où le quotient : 1,0*10^-3/3,9998*10^-25 = 2,5*10^21kg. Donc il y a 2,5*10^21 noyaux radioactifs dans un gramme de Plutonium 239.

Après, il faut multiplier le nombre de noyaux radioactifs dans un gramme de Plutonium 239 avec l'énergie libérée de la fission d'un noyau de Plutonium 239. D'où la multiplication suivante : (3,9998*10^-25)*(2,5*10^21) = 9,9998*10^-4 J. Ce résultat correpond à l'énergie libérée lors de la fission d'un gramme de Plutonium 239.

Enfin, on sait que la bombe atomique Little Boy pesait environ 4,5 tonnes et contenait 6,2 kg de Plutonium 239 dans le coeur de la bombe dont 1kg entra en fission et 1g se convertit en énergie. Pour calculer l'énergie libérée de cette fission, il faut multiplier l'énergie libérée d'un gramme de Plutonium 239 par 1kg. Nous n'avons donc pas besoin de convertir quoi que ce soit. D'où la multiplication suivante : 1,0*4,4765*10^11 = 4,4765*10^11 J.

L'énergie libérée par Fat Man était donc de l'ordre de 447 650 000 000 J soit 8 fois plus grande que Little Boy !

Elle fit toutefois moins de morts à cause (ou grâce) à la nature vallonnée du terrain de Nagasaki.

Champignon atomique suite à l'explosion de Fat Man à 550 mètre au-dessus de la ville

Réplique de Fat Man au musée national des forces aérienne américaine ( "Fat Man" atomic bomb at the National Museum of the United States Air Force)